Mapping the World with Art Review

South America drawn by the Artist, 13.

One of our favorite curricula that we’ve used during the past year has been Ellen McHenry’s Mapping the World with Art (MtWwA).  I’ve had several readers email me curious about how we use it.  This week we finished our lessons and are working on the final project.  Here is my overview of how we used it and thoughts on the curriculum.

Overview:

I originally purchased MtWwA for Geography only, but soon realized that it’s a combination of geography, cartography, art and even a little history.  It works best for middle school and up (though my 8 year old enjoyed it when he was able to go at his own pace).  The book is divided into four parts: 30 Readings, 30 Map Drawings, 23 Activities, and a Final Project where students create a world map.

The Readings section begins with history of the first maps and guides the reader in how they’ve been developed through time – with earlier maps being less complex than later ones. The reader is taken on a journey to a better understanding of how and why maps developed from necessity and exploration from ancient Greece through modern times.  My children and I appreciated the perspective it gave us.  For example, we were impressed when comparing a map that was made when the Pilgrims landed in America in 1650 with a modern map on our wall – realizing how much more we know now and that 1650 was not that long ago!  The section finishes with a discussion of how GPS satellites have revealed the entire surface of the Earth to us.  Interesting.

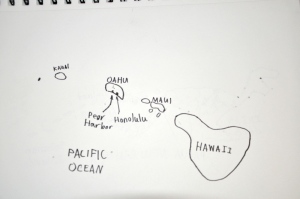
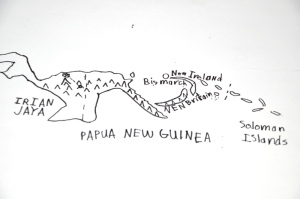
Next is the Map Drawing section intended for students to draw maps of countries and continents of the world.  In this portion each lesson shows detailed step-by-step instructions.  We purchased the optional DVD instructional video in which the author leads you through the map drawings.  It is interesting to hear the author’s take on each map.  At the beginning of each DVD lesson, the tools needed for that particular lesson are displayed on the screen so you know what to have available for that day.  (Tools needed throughout the course include a ruler, compass, protractor, pencil with eraser, large eraser, and a black waterproof pen.)

The third part is an optional Activities section which provides projects and reinforcement for the earlier topics.  Some of the activities include extra drawing practice, arts and crafts, games, and review worksheets.

Finally, there is a final project. It gives students the opportunity to put all the information they’ve learned together by creating a world map.  Templates are provided to photocopy to guide them along.

How we used it:

Like many people we don’t have unlimited time, so I chose Thursdays to cover only the parts of the program that I thought would work best for us.  We covered about one lesson per week consisting of the Readings and Map Drawing sections.   During our morning journal time, I’d cover the Readings.   This would often spark fascinating, meaningful discussions about both history and the level of understanding of the geography of the world for those who lived in earlier times.

In the afternoons we’d watch the DVD’s and follow along with the author whose knowledge on the subject was impressive.  The DVDs give you the option to pause to wait for everyone to have the time they need, and I’d also have the book open as an additional help if anyone wanted to see the drawings each step of the way.

We did not use the Activities section.

For the final project there are several options, and I chose the option of photocopying the 6 page templates to give the general idea how the continents and oceans fit together.  I thought this would best fit our goals and would keep frustrations to a minimum.  The final project is important to help students visualize how all the pieces they’ve drawn fit together as a whole.

When done in the time frame I used, some of the lessons may take multiple weeks to cover.  For example, Map Drawing 29 has parts A-G.  It took us 3 Thursdays to get through it.  Overall, it took us about 1.5 years to get through the entire book (with taking the summer months off.)

My thoughts:

We did not try to rush to get through this, and I considered it a fun elective.

Drawing the maps and thinking through the shape of the land helped them remember the information. In addition, we learned some more in depth drawing skills with compasses and protractors while sketching the continents and countries.  The final project drawing at the end helped cement the locations and gave us an important big picture view.  These factors combined with the fascinating history in the readings made for a positive educational experience.  For these reasons, I highly recommend Mapping the World with Art.

Cape Horn, by the Artist.

Do you see the ‘boot’ of Italy?

Australia, by the Investigator, 11.

Siberia, by the Investigator.

Hawaiian Islands, by the Architect, 8.

Papua, New Guinea, by the Architect.

Scary Monster, by the Explorer, 5.

Forming First Impressions: Kindergarten Math

The Explorer, 5, recently told me that his favorite subject is Math.  At this age he’s forming early impressions on the blank canvas that will become his Math Education.  Developing a strong base is important, but so is lighting a spark of interest.  Led partly by his fascination levels, I focus on three areas with my Kindergartener: math facts, new concepts, and problem solving.

1. Math facts

Mastery of the math facts will greatly reduce frustration for him down the road with things like muti-digit multiplication, long division, and many other areas.  It’s important that he learn the concept behind the idea.

I start him on skip-counting by introducing a hundred number chart.  After he’s learned to count to 100 (by ones), we learn the two’s, five’s and ten’s.  We then cover both odd and even numbers and what digits each type will end in.

We recently learned the three’s. For example:  I have him start at zero and count up three, and then cover the number with a rectangular counter stopping at 30 – for starters.  The idea is that he’ll begin to notice a pattern.  [He observed that the three’s have both odd and even numbers.]

Hundred number chart, counting by 3’s starting at 0.

Then he removes the counter and writes down the numbers – beginning at zero then up to 30.  (If he gets frustrated writing the numbers down, I just have him read them while I write them for him.) What I like about this is that not only does he learn to count by three’s, but he also realizes that it starts at zero.  He reads them forward and backwards a few times.  Then we focus on memorizing.

Recording the 3’s as he removes them

After he’s mastered the 3’s starting at zero, I then have him pick another starting number – say one.  We then count up by 3’s but notice that our numbers are now different depending on our starting point.

So far this year, we’ve covered the one’s (0 to 100); two’s (0 to 100); three’s (0 to 30); five’s (0 to 100); ten’s (0 to 100), the hundred’s (0 to 1000) and the odd numbers (1 to 21).  Next week we plan to start the four’s (0 to 40).  How many we’ll cover depends; I use his interest level to help guide me about how far to go.  It is not a race, though, and it’s far more important to me that he understands the idea.

2.  New Concepts

By this I refer mainly to the learning of the arithmetic operations:  addition, subtraction, multiplication, and division.  I often use a curriculum as my guide, and some of my favorites are Singapore Math, MEP Math, and Miquon Math.  However, I believe that any curriculum is a tool that should help and not hinder.  I often find myself filling in concepts that I think a curriculum should have spent more time on.  I use a Place Value Activity Kit to demonstrate all four operations.

We start by learning the plus and minus facts up to 10 (all the combinations), then we expand it up to 20.

Interestingly, we recently learned three different methods for subtraction. For example, consider:  15-8 = 7.

 Method 1: Start at 15 on our number line and count back 8 steps.  We stop at 7.

 Method 2: Think of 15 as a number bond of 10 and 5.  I ask my son if we can take 8 away from 5. (We’ve not learned negative numbers yet.)  He replies that we cannot, but we can take 8 away from 10.  So we calculate (10-8) and we still have our 5 from before so our answer is 2 + 5 = 7.

Method 2 demonstrated with place value kit

 Method 3: Start at 15.  Think about where our nearest ten is when subtracting. Answer:10.  Think about how many units we would take away from 15 to get to our nearest 10.  Answer: 5.  Then subtract 5 from 15 and next subtract 3 more. (15-5-3=7)

Method 3 explained.

Having learned three different methods hopefully causes him to analyze, compare, and develop a greater number sense regarding subtraction.

So far we’ve worked though the concepts of addition and subtraction mainly, and also a good start in multiplication.

Multiplication demonstrated with place value kit, and noting that ‘x’ means ‘groups of’.

More multiplication showing that multiplying can be thought of as repeated addition.

Having already introduced multiplication (with skip counting),  I then use examples like the one above with a place value kit to go into more depth by showing that multiplication is repeated addition and that ‘x’ can be thought of as ‘groups of’.  For division, I only introduce it with the place value kit and show how division is related to multiplication.

[As an aside: If a student is confused by a concept, I recommend trying another curriculum to explain it a different way.  Use the curricula that best helps your child understand OR simply explain it in your own words how you understand it.]

3.  Problem Solving

How I interpret it, problems solving means that a student has enough mastery of a concept that he can apply it to solve a problem.

Thus far for this type of activity, my favorite curricula are Singapore Math Intensive Practice and Challenging Word Problems workbooks.  What I like best about these are the way they encourage a child to visualize the problems in order to better understand and solve them.  Also, questions are asked from many different angles so that the child has to really think about what is being asked.

Recently we worked on a problem where he had to think about how a larger number can be made out of two smaller numbers to solve puzzle-like problems related to subtraction.  We pulled out our Cuisenaire rods to help visualize the combinations that make 10: (1,9); (9,1); (2,8); (8,2); (3,7); (7,3); (6,4); (4,6); and (5,5) – to remind us of our math facts. (Hopefully he sees the pattern that addition is commutative). Manipulatives can be a great addition when solving a complicated problem.

Looking for a pattern and using C-rods to visualize.

Of course, problem solving can also bring feelings of frustration. During these trials of deep thought, he grows in knowledge and develops math endurance.  I’ve found that giving praise when he’s solved a problem works wonders, and it’ll likely light a fire and make him want to learn more.

Overall, our plan is that we cover math fact practice and new concepts daily.  Problem solving (puzzle-type questions) may only happen two or three days per week.  We touch on all three areas every week.

It’s my intention that Math time be fun for him at this age.  Demonstrating that problem solving can be both rewarding and enjoyable [hopefully] paints a positive first impression.

AoPS Intro to Algebra Review – An Active Approach

For a middle or high school student who is motivated to take a more active role in learning Algebra, check out Art of Problem Solving Introduction to Algebra, 2nd Edition, by Richard Rusczyk.  Intended for students in grades 6-10, I’ve found it to be effective in not only teaching Algebra, but also in developing general problem solving skills.

Appearance

The pages are uncluttered with mainly black and white print and a few boxes highlighted in a peaceful blue – making it easy to follow and not distracting.

Jump Right In

Building concepts in a logical, step-by-step manner, the textbook is thoughtfully written to the student. The method appears to be this: the author carefully introduces new topics and engages the student by posing simple, related example problems, and then gives her a chance to jump in and develop her own solutions before presenting the answer to her.  For example, the chapter on quadratic equations begins by defining quadratic terms and expressions.  Then it leads the student by posing five such questions – gradually increasing in difficulty – related to quadratics.  This starts the student in the process of thinking about how she will answer the questions.  But the solutions are not revealed just yet.  The idea seems to be to motivate the student to reach her own solution before the book explains it to her.  Eventually the solution is explained, but by that time the student will be more aware of it, since she should have at least begun to construct her own.  Contrary to many textbooks I’ve seen, more up front thinking is expected of the student rather than being spoon-fed the material.  This active involvement makes learning math concepts less dull, more enjoyable and easier to remember.

Breaking It Down

Throughout the book there is a parallel with how new material is presented and the fact that complicated problems can often be solved by breaking them into smaller parts or steps.  For a quick example, when imaginary numbers are introducedand defined, the student is asked to evaluate a few simple cases on his own (which he should be able to do by applying the definition).  Next he is asked to solve aquestion that is slightly more difficult, but building off the previous question.  Then another – more difficult, but similar.  Finally, he is to simplify a set of more complicated imaginary number questions.  But if he has been solving the little problems along the way, the difficult questions are more easily diffused because he can break the difficult problem into smaller, simpler parts.  It no longer looks scary or confusing, and he will probably be able to quickly calculate the answer.  As I said above, only after he has had time to develop his own solution are the explanations presented in the text.  This approach makes sense, and is a helpful model for problem solving in general.

Following the above-mentioned example problems, there are Exercises that evaluate the concepts for each section.

At the end of each chapter is a thorough Summary section which highlights definitions, concepts, and/or other important information.  Many of the these sections also contain Problem Solving Strategies, and it is worth your time to read, absorb and apply these.  Next are Review Problems which seem to help measure how well a student understands the chapter.  And finally there is a Challenge Problems section in which will be found the more difficult problems that are likely to really stretch the student’s understanding and help her master the material.

Competitions

Problems previously seen in MathCounts, the American Mathematics Competitions (AMC8, AMC10, and AMC12,) the American Invitational Mathematics Examination (AIME), the USA Mathematical Olympiad (USAMO) and others are included in some of the exercise, review, and challenge problems.  Working these problems not only helps with understanding the idea of the chapter, but also in preparing for future contests.  In our situation, this book greatly contributed to the preparation of my daughter in past competitions.

Additional Helps

AoPS’s website also provides Intro to Algebra Videos which give the student another visual aid if desired.  Though my daughter did not use these, they are there if you would like them – which I appreciate.

There is a Hints section located in the back of the book for selected problems.  Any problem with a hint will note that at the end of the problem.

I strongly recommend the Solutions Manual.  It provides well written explanations with step-by-step solutions.

Caveats

It is important to read the How to Use This Book section at the beginning of the book for clarification.  A student should attempt solving a tough problem several times before looking at any hints in the back of the book.  For example, a student may work on a difficult problem for half of an hour or more, but not solve it.  She may feel frustrated and that she is getting nowhere.  But she is learning where her weaknesses and strengths are.  At some point she may want to look at a hint or review the concept notes of the chapter.

If you find that the lessons are taking too long, another option is to pick and choose challenge problems.

Highly Recommended

Overall, we thought highly of this book because there were challenging problems that made you think. 

The book seems creatively written with the intention of not only teaching Algebra, but also developing robust problem solving skills in its reader.  From the perspective of a teacher and especially if a student uses the materials as intended, I think it accomplishes this goal.

The Making of a Mathlete

I am often on the lookout for ways to broaden the horizons of my children, so this past school year I offered my 7th grade daughter the chance to take part in math contests.  She accepted.  In the fall, she took the American Mathematics Competition 8 (AMC), and this spring she competed in MathCounts.  As a home educating family why and how did we get involved in math competitions, and what was the experience like?

Why sign up? 

The biggest reason I considered this path was that I thought it to be a unique opportunity for her.  She is at ease with math, and I hoped she’d find it interesting.  Also, math competitions give students the chance to develop problem solving skills in a positive environment with others who share similar interests.

How to prepare for the AMC8

The AMC 8 is a 25 question, 40 minute multiple choice exam for middle school students.  Although it was easy to register for this competition,  I did have to locate a proctor.  I was fortunate to find a private school math teacher who gave her the exam.  The AMC 8 website also has additional locations for the AMC 8 at Higher Education Sites.  There is also a similar site for the AMC10/12.  If you want your child to take one of the AMC tests but cannot find a proctor, one of the locators may be worth a try.

To prepare for the AMC 8, she studied past exam problems from the AOPS Wiki.  This worked well for her, but you may also purchase past exams and solutions directly from the AMC website (see the Registration page).

How to prepare for MathCounts

We registered online and submitted a  ‘Homeschool Participation Attestation’ form in early fall.  To be eligible, a student must be in 6th, 7th, or 8th grade.  The process was relatively simple, and we had no problems entering her to compete as an Individual.  Homeschool Teams are also eligible to participate.

Once registered, they mailed us a packet which included the MathCounts School Handbook.  This is one of the several resources my daughter studied (another being Art of Problem Solving textbooks).   The earlier you sign up, the more time you’ll have to prepare.

Since we educate at home, I chose to be her coach.  Parent as coach is something to carefully consider, because it is a time commitment.  We set Fridays as our competition prep day and used Sunday afternoons to go over any problems that needed more discussion.  Another option to consider, depending on the laws in your state, is that you may also be able to find a local public or private school team for your child to join.  There are advantages to each case.

What was the actual contest like?

The contest consisted of a Sprint, Target and Team Round.  These rounds extended to about two hours total including breaks.  The Sprint Round was 40 minutes (30 questions).  The Target Round was about 30 minutes (8 problems in four pairs at 6 minutes per pair) and the Team Round was 20 minutes (with 10 problems solved by a team).  After this mental workout, the students were treated to a pizza lunch while the scores were calculated.  Following lunch, the top scoring 16 students were asked to move to the front to compete in what is known as the Countdown Round.

As the only event open to the public, The Countdown Round was a fast-paced, oral competition in which the students were then called two at a time up to a table in front of the 130+ students, coaches, and spectators.  These two competing students were asked a question on the overhead screen and were given only a short amount of time (about 45 seconds) to answer.  No calculators were allowed.  Once she had figured her answer, she had to respond by first pushing a button and then waiting to be called upon.  The first student who answered three questions correctly remained in the front to continue on to the next round.

It was exciting to watch the Countdown Round.  I’d never witnessed anything like it before.  I was impressed with the bravery the students displayed – competing in front of a large group of onlookers…answering tough questions…under strict time restraints!

The top three Teams, Individuals, and Countdown Round competitors received a trophy.  In addition, students who make it to the national level may even win scholarships.

*Contest Results* 

The preparation paid off.  I’m happy to report that my daughter did win a MathCounts trophy.  It was inspiring to see her be rewarded for her efforts – with several of the students congratulating her.  This encouragement has convinced her to continue, and she will be back to training this summer and fall for the next contests. 

Though it was not an easy thing to prepare for, I’m glad she agreed to take part. The sacrifices were worth it; I think it was a positive experience for her.

If you have a child who enjoys a challenge and would like to be around others interested in Math and Problem Solving, these competitions may be for you.

* Other Math Contests and Programs from the AMC

* List of worldwide Math Competitions from the AoPS Wiki

**2013 Parenting the Gifted Blog Tour**

MEP Reception – A Thoughtful Introduction to Math

Are you looking for an introductory math curriculum with a strong focus on thinking for your 4 to 6 year old?  Consider MEP Math – Reception, a FREE printable curriculum based on a Hungarian Kindergarten Math program.  MEP has been developed by the Center for Innovation in Mathematics Instruction “to enhance the mathematical progress of students in primary schools.” See this page for more background information.

Last month my four year old completed the 60th and final lesson, and here are some things I like about MEP Reception:

*  Counting:  Students are introduced to numbers up to ten, but the emphasis is not on the reading or writing of numerical digits.  Instead, for example, when the number six is discussed a student may write six dots or tally marks, clap six times,  knock on the table six times, or count out six objects (counters).  The writing of digits is postponed until Year 1.

*  Observation:  In an early lesson, a student is given colored sticks or toothpicks.  He is asked to look at a picture and study shapes made out of colored sticks and think about how many of what color toothpicks are needed to make the table, chair, tree, etc.  He then recreates the pictures on his own with care to make the same shape and use the same color sticks.

*  Mental Operations:  Students are asked to listen to a story, think of an answer but wait until called upon to say it.  For example, an earlier lesson says, “Two rabbits were playing in the clearing, then a rabbit joined them.  How many rabbits are there now altogether?” (Pause and wait and then ask for the answer.)  This is my one of my favorite parts of Reception, because it trains him to think of the answer and hold it in place before saying the answer.  Over time the difficulty level of the these questions increases, and towards the end of  Reception comes a question like this:  “A monkey had ten bananas.  He ate two bananas first, then three bananas, and then one.  How many bananas remained?”  This all takes place mentally without writing it down, which I see as a plus.  (It is okay if the child wants to draw a picture of what is happening after thinking about it for awhile to help him solve it, but this program really gets him to think about things rather than simply being told what to do and how to solve it immediately.)  Another question asks the following: “Ann, Ben, and Celia collected shells.  Each of them collected three shells.  How many shells had they collected all together?”  In the last example, multiplication is being introduced.

*  Games: Reception uses games throughout to make learning more engaging.  When played well, the student forgets its math time and focuses on winning the game (and meanwhile is learning addition or subtraction depending on the game.)  For example, in one game the student is to put a dog (or some counter) on a colored square to begin.  She throws the dice and moves as many steps as the number of dots she rolls on the dice.  Later the game is played again but modified so that now the player moves one more space than the number on the dots rolled on the dice.  To win, you must throw the exact number needed to get to the bone when you get close enough or you will lose your turn.  The student will be so focused on winning that she will forget that she is learning the +1 addition facts!

In another game, a student throws the dice and if a one, three, or five (odd number) is rolled, he may move that many place to the right or left.  If a two, four, or six is thrown, he may move that many places up or down.  He must also say aloud the number of spaces and the direction.  The first player to reach his colored square on the opposite side wins.  This game mentally separates the odd and even numbers on a dice without formally discussing ‘odd’ and ‘even’ numbers.  It is guiding the student, I think, to make a distinction between those two groups of numbers for a reason to be revealed at a later time.

*  Ordinal Numbers: Students are asked when looking at a line of people about who is the first, second, third, fourth, and then it jumps to the question of who is the fourth from the end of the row, first from the end of the row?, etc.  It goes from simple to more complex questions gradually.

*  Sets: Set theory is gently introduced.  For example, one lesson asks the student to notice a certain set of mugs in a group.  It asks how many are colored, and then how many are not colored.  Also the mathematical symbols often used with set theory, intersection and union, are creatively placed on sheets to be traced – building a student up to these ideas by using both thoughts and symbols.

*  Geometry: Geometric shapes introduced are mainly circles, quadrilaterals (including squares and rectangles), triangles, and few others types to show the distinction from the former.  Students are expected to analyze the shapes that make up a steam engine in one lesson.  Then they are asked to color them the same color they are on the train.  Next they’re asked how many circles, quadrilaterals, triangles, and total number of shapes to build it.

* Decomposing:  A student is asked to think of how many different ways can we divide ten counters between two people.  All the combinations are demonstrated: 10,0; 9,1; 8,2; 7,3; 6,4; 5,5; 4,6; 3,7; 2,8; 1,9; and 0,10.  Students will possibly see the pattern of what is happening after arranging the first few combinations.  Also, if the student notices that combinations can be reversed (3,7 and 7,3) , this would be an opportunity to demonstrate the Commutative Property of Addition – that is – the order of addends doesn’t change the sum.

*  Sequences: Sequences appear towards the end of Reception.  Any counters/shapes/etc. can be used to make a pattern that repeats, and the student is asked which shape or color of counter would come next.  (I used Teddy bear counters of different colors to make patterns for my son.)  Later, numbers are said in patterns, and the student is asked to repeat (say) the number pattern. Singing it in a chorus may help him remember it.

* Making Figures: This was my son’s favorite part.  Paper is folded and shapes are drawn on the fold to be cut out by the student.  The last lesson contains many of these, and it promotes spatial skills and the idea of symmetry.

What I view as Reception’s greatest strengths are the mental development of operations and the focus on thinking throughout the program before the writing of words and numbers is ever introduced.  Ideas are developed in small, purposeful steps with the depth expanded leading to more complicated concepts over time.  Things are happening for a reason even if the child may not see where he is being led.  I was impressed with the thinking skills it encouraged in my son, especially with the development of mental operations.  We had fun playing the games, and he was so determined to win that he forgot he was learning math.

It is teacher intensive, and I do recommend reading the lesson ahead of time for preparation to understand where the authors are going with the concepts and to locate any needed manipulatives, counters, etc.

MEP Reception is a gentle and thoughtful introduction to Mathematics for little ones.  If you would like to learn more about it, I recommend starting here and spending a little time reading through the introductory material.  You may also read an earlier review I wrote, MEP Math – For a Change (An Early Review).

Beast Academy Review

Are you looking for a fun way to interest your child in Math?  If so, then Beast Academy, a new elementary math program from Art of Problem Solving, Inc., may be for you.

Beast Academy 3A, 3B, and 3C Guide and Practice books.

Written in an engaging graphic novel format, the Beast Academy 3A, 3B, and 3C Guides follow friendly monsters as they learn about Math and participate in competitions.  Here is an example of an excellent Guide page.

A Venn diagram showing the relationship between some shapes.

Each Guide has a corresponding Practice book containing the written work.  The Practice book pages are in black and white, which I like since it is less distracting for a student.  Here is a sample page from 3C.

A Practice page from 3C demonstrating the subject of Variables by showing illustrations of balancing scales.

The first page of each chapter in the Practice book contains a helpful sequence for the Guide and Practice book.

The sequence for Guide and Practice.

The problems usually start out simple so the concept can be digested gradually, but can then become more challenging.  The challenging problems are usually marked with a star.  For these there are hints in the back of the Practice book, but students are encouraged to attempt the problems for awhile before looking at the hint.

Hints section in the back of the Practice book.

All Practice books contain an impressive solutions section which sometimes gives two different ways to solve a problem!  Many parents will find this valuable, and some students will appreciate that there can be more than one right way to answer a question.

Solutions section located in the back of the Practice books.

My son has completed books 3A, 3B, and is currently working through 3C.  One of the things I like about these books is the way students are guided to think more creatively about how to approach a novel problem.  The monsters work together and point out clever ways to approach problem solving.  Examples of this are in the below photo on skip counting.  The student is able to see that doing so can make a seemingly difficult task easier.

From Guide 3A, the monsters are coming up with creative ways to skip count.

The books are also helpful for visual learners or anyone who may benefit from having a visual aid when a new idea is introduced.  The little monsters often refer to things a child may be familiar with – for example, letters and houses to teach angles – making the concept easier for her to learn and remember.

Monsters using letters made from toothpicks to demonstrate angles.

Monsters showing how angles are all around us and why they are important.

The books are aligned with the 2010 Common Core Standards, but also go into more depth of concepts than I have seen in other similar age curricula.  In fact, some of the problems may leave the student feeling perplexed. Often after taking a break, he may return to the problem more determined to solve it.  This has been the case with my son.  He has learned a lot, and he continues to enjoy these books.

The books can be used as a full curriculum, but I have been using them as enrichment so far.  For now the first three of four parts are available for grade 3 with the fourth part, 3D, due in January 2013.  According to the website, eventually there will be a complete second through fifth grade curriculum, published in the order of 4th, 5th and then 2nd.

There are additional Resources including Coloring Pages, which I have used with my younger son to help familiarize him with some of the beasts.  As with most curriculum, it is beneficial to have your child take a Pretest Assessment before you begin for proper placement.

As in real life the monsters don’t always win every math competition. Yet they are supportive of each other and determined that losing is an opportunity to come back stronger next time.  What a great message!

They’ll be back!

So if you’d like to add a little spice to Math time, try Beast Academy!

MEP Math – For a Change (An Early Review)

For elementary math I want to shake things up a bit this year.  So I have been experimenting with an online free British math program called  Mathematics Enhancement Programme. From the website, MEP is a resource from the Centre for Innovation in Mathematics Teaching. “The Centre for Innovation in Mathematics Teaching (CIMT) was established in 1986. The centre is a focus for research and curriculum development in Mathematics teaching and learning, with the aim of unifying and enhancing mathematical progress in schools and colleges.”  

For the past two weeks, I have been trying out Years 5, 2, and Reception with my soon to be fifth, second and preK grade children.   To get started, I first went out and bought some new printer cartridges and printed out the course pages for the first thirty lessons for each of the three levels.  For Reception color ink is necessary for the Copymasters, but black ink cartridges are all that is needed for the Lesson Plans, Practice Books and Copymasters for the other levels.  (Note: color ink is necessary if you print off the OHP Transparancy Collection.) I then printed off the Number, Shape, and Sign Cards, Shape Cards with Dots, and Number Lines and had them laminated.   Once all of the printing was done, I then read the lesson plans the night before and get out materials that will be needed.  I store the ‘not in use’ Lesson Plans in binders for each level so that they can possibly be reused at some point, and I keep the daily ‘weeks worth’ of Lesson Plans, Copymasters, and Practice Book worksheets in separate folders so that I can quickly get to them for each child.

My four-year-old has made it through the first twenty lessons of Reception.  I so far have liked the focus on thinking and the fact that the lessons have only a little writing.  The colorful Copymasters include conversations about a family we meet over and over throughout the advancing lessons and games that make the math more engaging for him.  I do substitute some of my own manipulatives from other math curriculum I own to adapt the games at times.   After two weeks of experimentation,  I have decided to continue on with MEP for him and finish the next forty lessons.

My 7 year old has also made it through the first twenty lessons of Year 2.  As a positive, MEP uses proper mathematical vocabulary and introduces other concepts (like Roman Numerals, less than or equal to, greater than or equal to, and combinatorics) much earlier than I have seen in other programs.  It is spiral, so the concepts get revisited often, but more thinking is needed from the student when concepts are introduced compared to other spiral programs I have used.  There are some problems where the student has to really think about and look for a pattern versus being told how to do it, and then being expected to just memorize what to do.

My 9 year old has completed the first ten lessons of Year 5. Each lesson at this level has a many concepts going on throughout, so I’ve found it best to only do one/at most two lessons per day with him.  I have found things come up in MEP Year 5 that he has not yet seen – for example, graphing intervals on a number line including endpoints.  For this reason, we are progressing at a slower pace when new concepts come up.

As with the other levels of MEP, I see the necessity for the student to think or figure out the pattern when an idea is initially introduced to be a positive.  My favorite parts of this program are the consistent use of correct mathematical vocabulary and set notation from the start, the way the program encourages thinking with the presentation of concepts, and the continual application of the concept over time.

With what I have seen so far of Year 5 (the first ten lessons 😉 ), I think the CWP and IP books in Singapore Primary Maths contain more challenging word problems.  For this reason, I plan to continue using them alongside MEP Year 5 as we continue moving forward with this program.

Overall I have been happy with what I have observed in MEP.  It is very teacher intensive, and I have found it helpful to be ready both mentally and with having any manipulatives set up for a smooth lesson.  There have only been a few small errors (possibly typos) so far in the Year 5 Lesson Plans and some of the Lesson Plan problems do not line up exactly to particular problems in the Copymasters and Practice Books, but I did not consider these to be major issues.  We also replace the money signs in MEP with $ signs, and I cover money in more depth with Singapore Math Standards as well.

For these reasons, I have decided that we will continue on with MEP in the fall combined with the more challenging parts of the Singapore Math Programs and the other adjustments mentioned.  I am sure I will have more to say about it as we get further along.

There is also an MEP Homeschoolers Yahoo group which I have found to be helpful in getting started with tips and files which answer many questions.